Beautiful Mathematics: A Discussion between Author and Mathematician
Johanna AirthMasahiko FujiwaraYoko Ogawa
A foreword from Amanda—
A few months ago I read a novel called The Housekeeper and the Professor, by revered Japanese writer Yoko Ogawa, translated into the English by Stephen Snyder in 2009. A writer friend had recommended it on Facebook and, seeing it dealt with mathematics, I had to read it. The Housekeeper and the Professor is about a single mother who is sent by her employers, a housekeeping agency, to work at the home of a mathematician: “the Professor”. Since an accident a number of years ago, the Professor has short term memory loss, and can only remember new things—or people—in 80 minute cycles. He sees beauty in the world through patterns of numbers—including amicable numbers, primes, and zero—and our narrrator and her 10-year old son (called √ , or ‘Root’, by the Professor) can’t help but to see the world in this new way.
As readers, we open our eyes along with her. I’ve never enjoyed maths, but this book gave me new ways to experience it, enabled me to find beauty where previously I had only felt fear, or detachment, or self-loathing. (And yes, these are some of the ways I deal with maths.) In this way, Ogawa’s book has changed me. It’s a wonderful quiet read: the sound of pencil on paper, rain outside, baseball on the radio, the warmth of tea in a lovely cup. It’s medicine for our busy, disrupted lives. Ogawa’s story reminds us to be open, not just to new ideas, but to those unexpected connections we make with others, that fill holes we forgot we had, and in doing so, sustain us.
I had to learn more. Amongst countless reviews of the book and interviews with Ogawa—who is quite famous in Japan—I came across this short blog post by translator Johanna Airth, which introduced me to yet another book, “Yonimo Utsukushii Sugaku Nyumon” (Beautiful Mathematics). A conversation between Ogawa and the mathematician Masahiko Fujiwara. It was not translated into English.
Thank you to Johanna Airth (translator), Yoko Ogawa and Masahiko Fujiwara and their publishers, we are fortunate to be able to publish two excerpts from this book in English, for the first time. The entire translated Table of Contents for the book is available at the end of the post. Johanna, by the way, is not only an avid reader, writer, and translator—but a mathematician, too!
The preceding is an excerpt from “Yonimo Utsukushii Sugaku Nyumon” by Masahiko Fujiwara and Yoko Ogawa and was first published in Japanese by Chikuma Shobo Co. Copyright © 2005 by Masahiko Fujiwara, Yoko Ogawa.
Beautiful Mathematics: A Discussion between Author and Mathematician
By Masahiko Fujiwara and Yoko Ogawa
Translated by Johanna Airth
Chapter 3: Japanese Aesthetics: The Universe in a Haiku
Ogawa: Coincidentally the word “haiku” came up just now. Abstract mathematical concepts are expressed concisely, in an equation of one line. In that sense, it is similar to Japanese haiku, in which the 5-7-5 format offers an extremely condensed expression of our awe of nature.
Fujiwara: There are many defining components of mathematical beauty. But I do believe one such aspect is the ridding of demons, if you will. A complex idea is turned into one line. This process of identifying an idea’s core is tremendously exciting and beautiful. In that sense, I agree, it is similar to haiku.
Ogawa: I feel it is a practice unique to Japanese culture.
Fujiwara: I don’t believe many Japanese people know this, but amongst the sciences, mathematics is the country’s strongest subject. It is my belief, that of all the humanities, literature is the country’s top subject, followed by mathematics a few steps behind. We fare far better in mathematics, relative to other subjects such as physics or biology.
This has been the case since the Edo era [1], when Japan used ‘wasan’ mathematics before the introduction of Western mathematics. That isolation period saw two mathematical geniuses emerge: Sekitaka Kazu and his mentee, Takabe Katahiro. Then during the Taisho era [2], Takagi Teiji published his findings on class fields theory and ranked amongst the top mathematicians in the world. This was around the time of World War I, when all academic collaboration with Germany, a major intellectual hub, was stopped. Takagi discovered his findings on his own.
I believe that Japanese have a strong basis in math because of their keen aesthetic sensibility. Oka Kiyoshi, another mathematical genius who passed away about twenty years ago, believed Japanese aesthetics was cultivated through haiku - the practice of expressing the vast beauty of nature in a 5-7-5 format. From a young age, we are taught to convey our surroundings, our world, our universe, in 17 words. Take the famous haiku by Basho:
Turbulent the sea
Across to Sado stretches
The Milky Way
The poem makes you see into the stormy ocean that is right in front of you. Then it takes your gaze off into the horizon where the Sado Isles lie. It relates this stretching distance to the Milky Way that extends across the sky, taking your imagination far out into space. Oka believed mathematics requires originality - an imagination that takes the gaze far out into the universe.
[1]-Edo era: 1603-1868
[2]-Taisho era: 1912-1926
Chapter 9: Beautiful Theorems, Ugly Theorems
Ogawa: You mentioned there are ‘beautiful’ theorems in our meeting earlier, citing the well-known theorem: the sum of angles in a triangle is always 180º, as an example. You also said, there are ‘ugly’ theorems. Could you give us an example? I don’t quite understand how a theorem could be ‘ugly.’
Fujiwara: Here is one such, ‘ugly’ theorem: excluding 0 and 1, there are only four numbers in which the sum of the cube of its digits, is equal to the number – 153, 370, 371, 407.
To demonstrate,
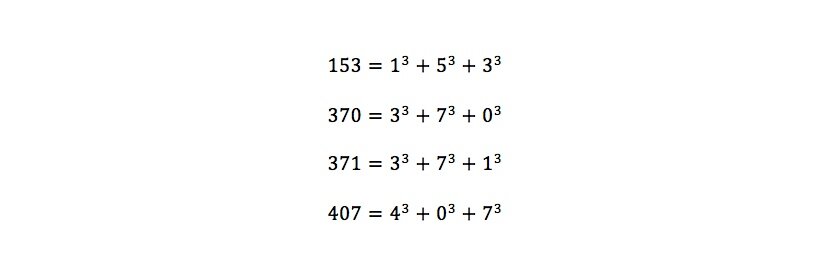
No matter how far along the number line we look, there are only these 4 numbers that satisfy this condition. Yet, explaining how this is ‘ugly’ is a bit difficult…
“The sum of angles in a triangle is always 180º,” is a model of elegance, and there a many such beautiful theorems. To share another: let us add all the odd numbers, 1+3+5+7+… and so forth. You can stop anywhere on the number line, and that sum of odd numbers will be a square number. The proof is equally as beautiful as the theorem.

We can continue forever, and every time you add an odd number, we can form a square, or said another way, we get a squared number. Therefore, the sum of odd numbers from 1 to 2n-1 (where n is a natural number) is:
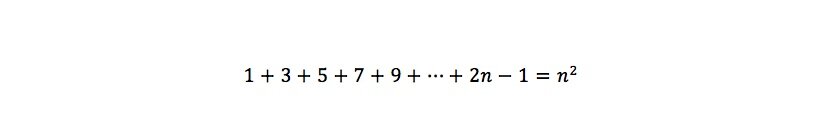
It is quite an elegant proof.
To give you another example of what I would call an “ugly” theorem – this is one I have discovered. Take the number 1729. Add up all the digits: 1+7+2+9 and we get 19. Now take that sum and switch the digits around to make 91. Multiply 91 by the previous sum of digits, 19 x 91, and you are back to the original number: 1729. The number 1458 also has the same characteristics. Add the digits: 1+4+5+8 =18. Flip the digits and multiply the two numbers: 18 x 81. We are back to the original 1458.
This is also true for the number 81. Excluding the number 1, there are only these three numbers that have this quality.
Mathematicians don’t think much about this find. If there are beautiful theorems, it is only fair that ugly theorems exist. The theorems I discover usually fall under the latter category…
Ogawa: Is it flipping the digits around, this turning the number upside down, that makes it ‘ugly’?
Fujiwara: More like, why do you have to flip the digits at all – what is the point of it? And afterwards, why do you have to multiply the swapped numbers together? But at the same time, there is something special, because of all the numbers that span infinitely, there are only these 3 that have this quality.
Ogawa: And this is something you have proven!?
Fujiwara: Yes, I proved it almost the moment I discovered it. But the proof requires a lot of nasty number crunching. It doesn’t have the elegance of the previous proof - lining up the pebbles into squares. If the proof isn’t elegant, already there is no real value in it.
Ogawa: But you must have been happy when you proved your discovery?
Fujiwara: True. I was happy I could explain the logic behind it. But after a while, my work started looking like something ‘disposable,’ and that didn’t make me feel very good about it. I have never admitted that to anyone…
Ogawa: That makes this, a precious conversation!
Fujiwara: But Ogawa-san, I think you do understand why that discovery was ‘ugly’; just now you asked about the switching of the digits - you questioned its necessity. I think you have a good sense of mathematical aesthetics.
Ogawa: Oh, no. I hope I didn’t offend you. But I understand how important this goal of attaining beauty is – otherwise there is no getting through the grueling research to prove a theory.
Fujiwara: It can be quite disparaging when your research isn’t going anywhere.
Ogawa: Mathematical results then, must be binary: zero or perfect.
Fujiwara: There is no midpoint. You are never satisfied with, “well I got up to this point,”; we strive for perfection. Yet too often we lose faith and give up. You see, mathematicians, even those we call genius, are all prisoners to our own inferiority complex; the work is never good enough. I have three sons, and I want them to grow up to be anything but a mathematician.
Ogawa: Your sons are all so studious and good looking! I was told one of them was even scouted by Johnny’s, the talent agency[1].
What is the most important factor in making a mathematical discovery?
Fujiwara: You have to tinker with it. For a numerical discovery, play with the number. Put the number in your hand and let it roll around; add to it, subtract from it, flip the digits around, use your imagination on it. Maybe you start to see something. Then you go to work. You do extensive experiments on it. And if that holds, then you work to prove it. Most of the time, the proof is like taking candy from a baby, because by then you know the number so well. But first you must tinker with it. It’s the most crucial and influential step in a creative process. In literature, you can read a beautiful passage, appreciate it, and even understand it. But it doesn’t become this treasure you keep within your soul, unless you memorize it, say it out loud like a prayer, and play around with the words. It is the same for geometry; you tinker with it, draw all different kinds of shapes while thinking, “This isn’t it,” “Nope, not this either,” until something happens.
This ability to tinker is a common trait amongst mathematical geniuses. And it’s not only observed in how they practice math. They read and memorize old Chinese text. Their mothers would recite stories, which they would memorize. Take Takagi Teiji, the globally recognized mathematical genius during the Taisho period. I recently went to his birthplace in Gifu prefecture to do some research on him. From three up until six years old, he didn’t practice math at all. Instead, he was reciting classic Chinese texts, and reading stories. And he would memorize them. His mother would bring him to a temple, and he would memorize the prayers of Shinran, that monks in training would learn. I believe it was this practice of recitation that led him to his own creativity. We mentioned Srinivasa Ramanujan[2] before, the famous Indian mathematician, and he was the same. His mother had memorized old Sanskrit epics of ancient India, the Mahābhārata and the Rāmāyaṇa - stories over a thousand pages long. She would recite these stories to her son, and he in turn memorized the epics. He would repeat it over and over, just like his mother did, as if he were humming a song.
Ogawa: It is unfortunate the recent view on education has cast such an unfavorable light on rote learning, or memorization. There is something transformative about inviting a text or a number into your subconscious and making it a part of you – into your own treasure. I believe such aspect of memorization is necessary in our education.
[1] A talent agency well known in Japan for discovering Boybands.
[2] Chapter 5 : Conditions of Genius
Table of Contents:
Forward by Yoko Ogawa
Part I: If it is not Beautiful, it is not Mathematics
1. The Romantic Mathematicians
2. Purity of Unapplicable Mathematics
3. Japanese Aesthetics: The Universe in a Haiku
4. Timeless Truths
5. Conditions of Genius
6. “The Housekeeper and the Professor” and Amicable Numbers
7. The Monumental Discovery of Zero
8. Perfect Numbers, and a Japanese Baseball Player
9. Beautiful Theorems, Ugly Theorems
10. Fermat’s Theorem
Part II: The Hidden Order
1. The Elegance of Triangular Numbers
2. Mathematics as an Experiment
3. The Mysterious Relationship Between Geometry and Algebra
4. Indian and English Mathematicians
5. Primes: Beautiful Order Within Chaos
6. The Infinite World of Primes
7. The Devil’s Problem
8. The Occurrence of Pi Without a Circle
9. Peeking at God’s Notebook
Afterwards by Masahiko Fujiwara
Feature image by Petr Glivický